Problem 4b
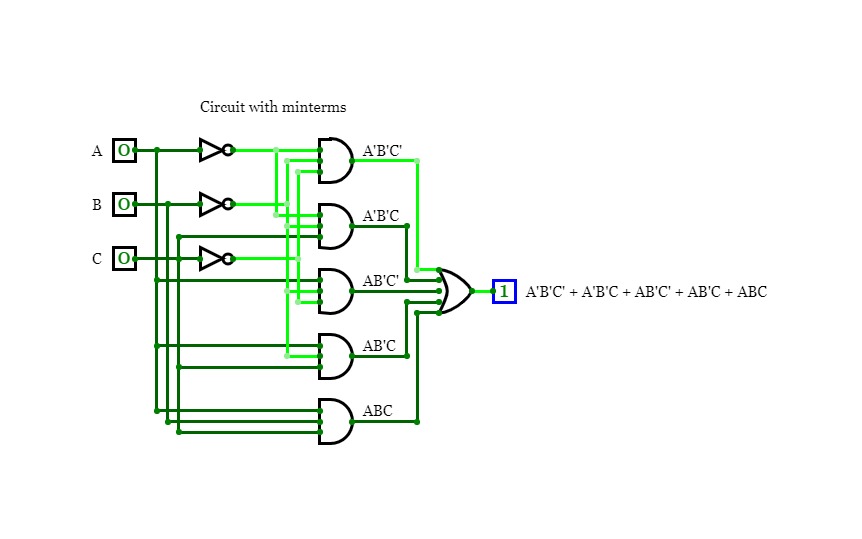
Problem 4bConsider the function F(A, B, C) = Σ m(0, 1, 4, 5, 7).
b. Draw the circuit of the function in part a.
Problem 4d
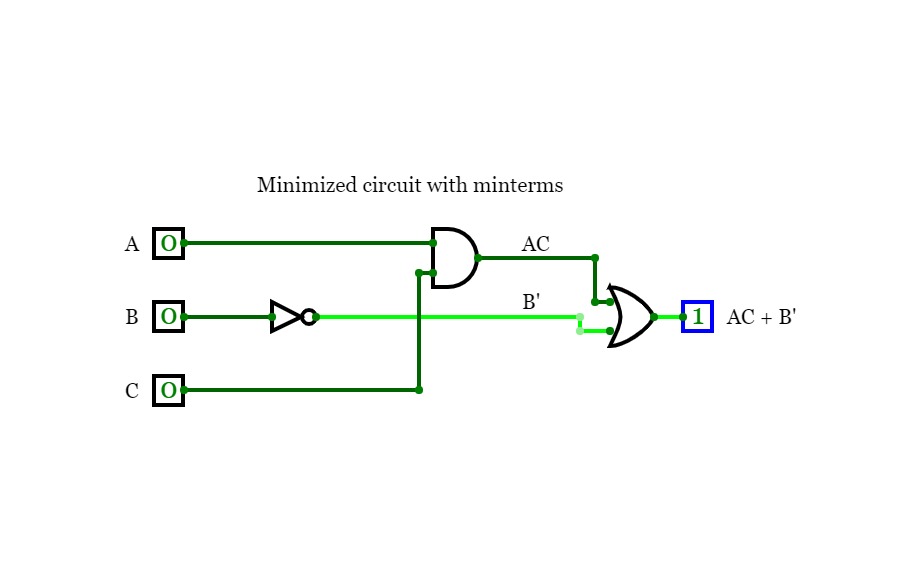
Problem 4dConsider the function F(A, B, C) = Σ m(0, 1, 4, 5, 7).
d. Draw the circuit of the result from part c.
Problem 5b
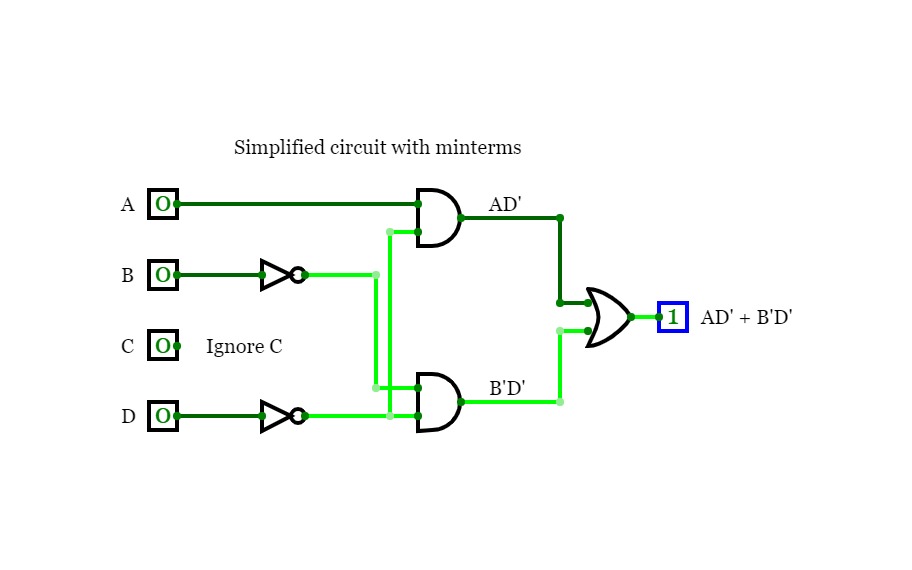
Problem 5bConsider the function F(A, B, C, D) = Σ m(0, 2, 8, 10, 12, 14).
b. Draw the circuit of the result function from part a.
Circuit 3.1
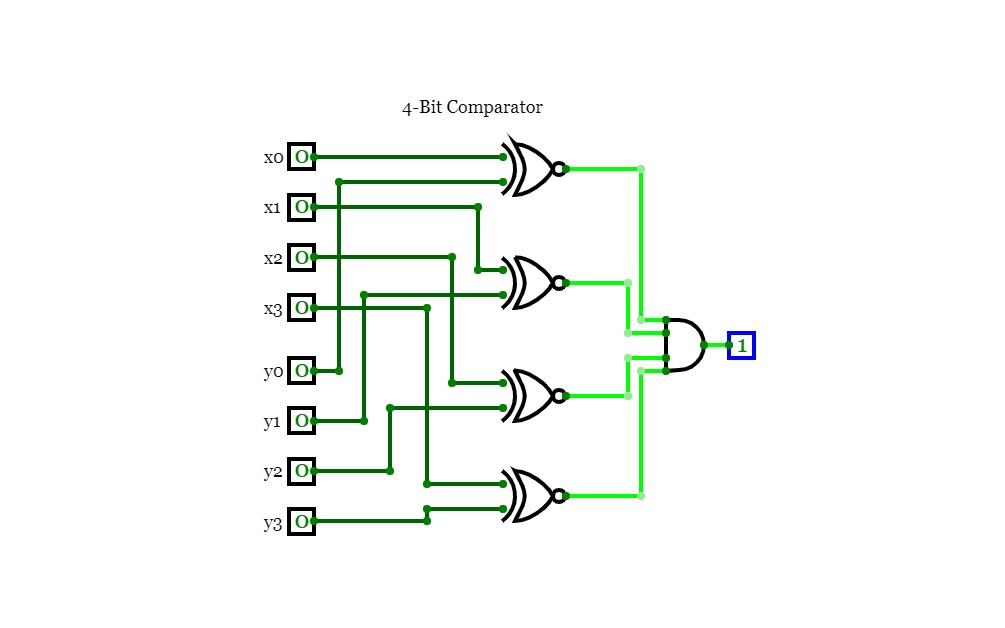
Circuit 3.1Design a circuit that takes as input two 4-bit numbers x and y and produces a single bit in the output, such that when x = y its output is 1, and when x ≠ y its output is 0.
Hint: use four XNOR and one AND gate.
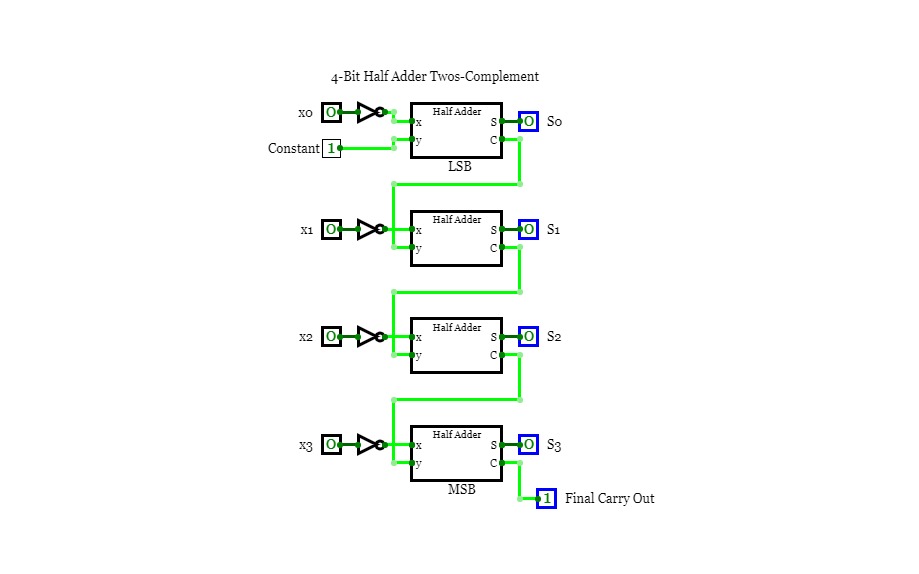
Circuit 3.2
Circuit 3.2Use 4 HALF-ADDERs to build a circuit that takes as input a 4-bit number
x and on its 4-bit output computes the twos-complement of x.
Hint: first use a layer of INVERTERS to invert the input of x to produce the ones complement of
x, and then add to this the value 1 to produce the two’s complement.
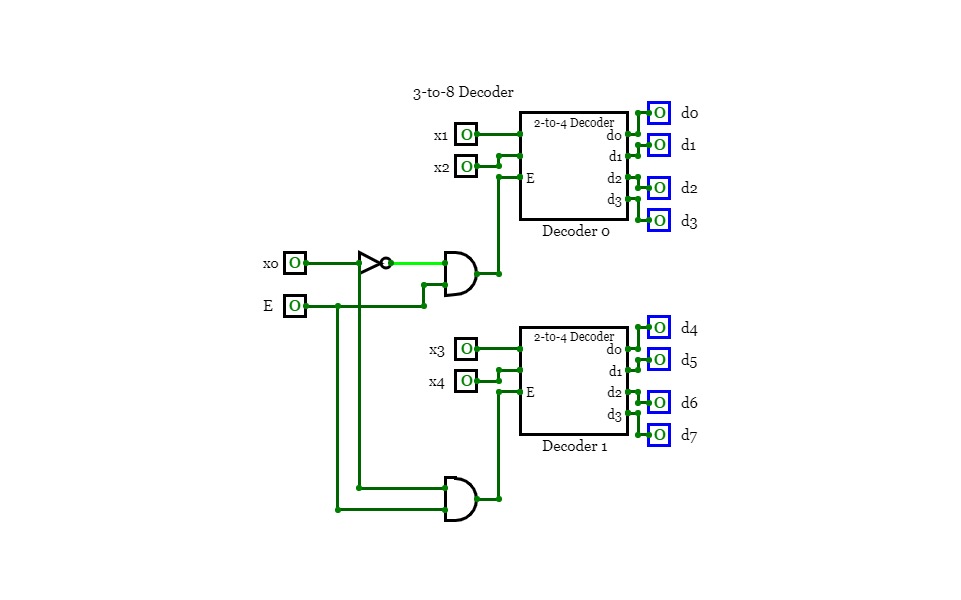
Circuit 3.3
Circuit 3.3Use two 2-to-4 DECODERS (with Enable bits) one INVERTER gate and
two AND gates to implement a 3-to-8 DECODER (with Enable bit).
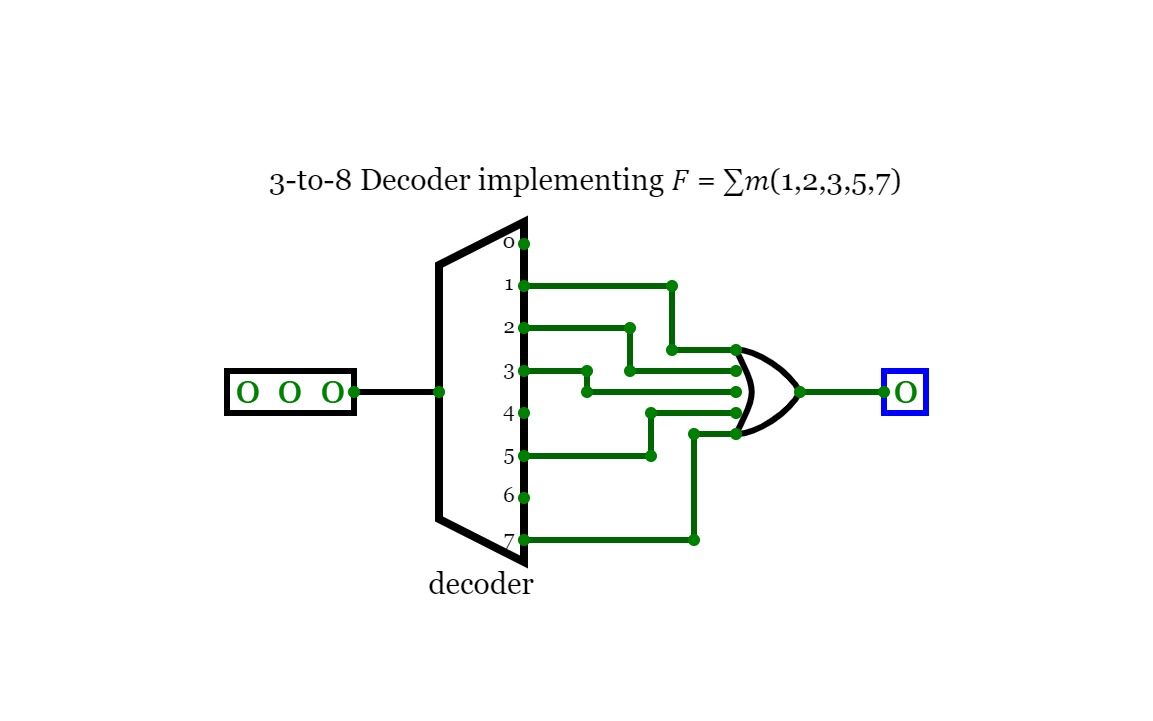
Circuit 3.4
Circuit 3.4Use a 3-to-8 DECODER (and an OR gate) to implement the following
function: 𝐹 = ∑𝑚(1,2,3,5,7).
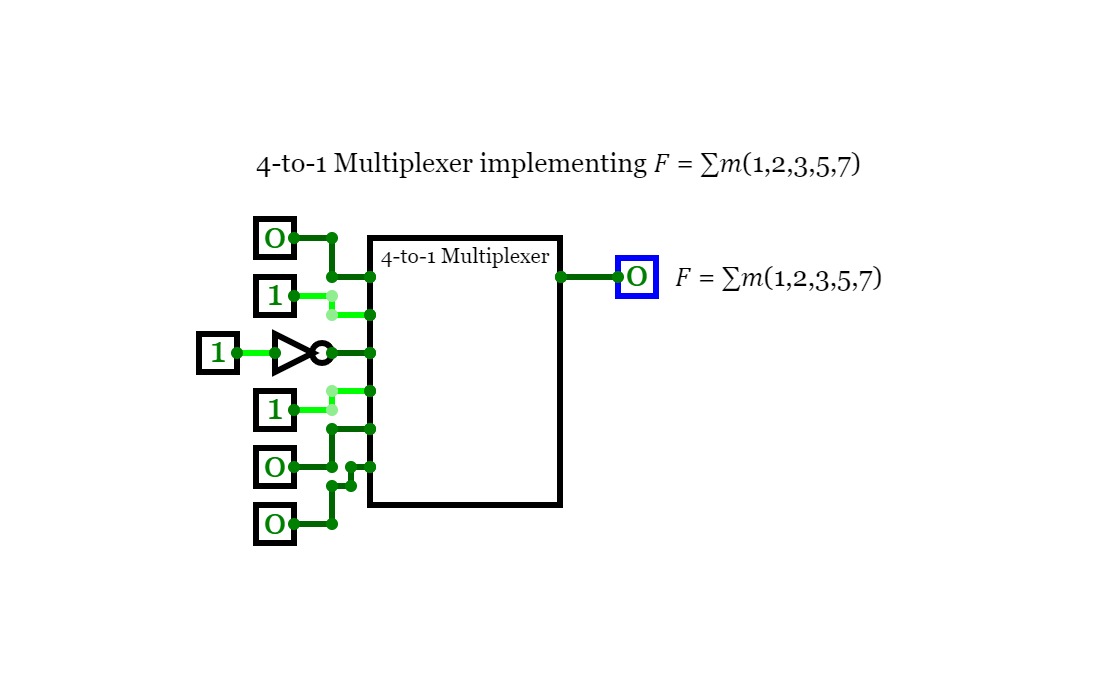
Circuit 3.5
Circuit 3.5Use a 4-to-1 MULTIPLEXER (and INVERTERS if needed) to implement the following function: F = ∑m(1, 2, 3, 5, 7).
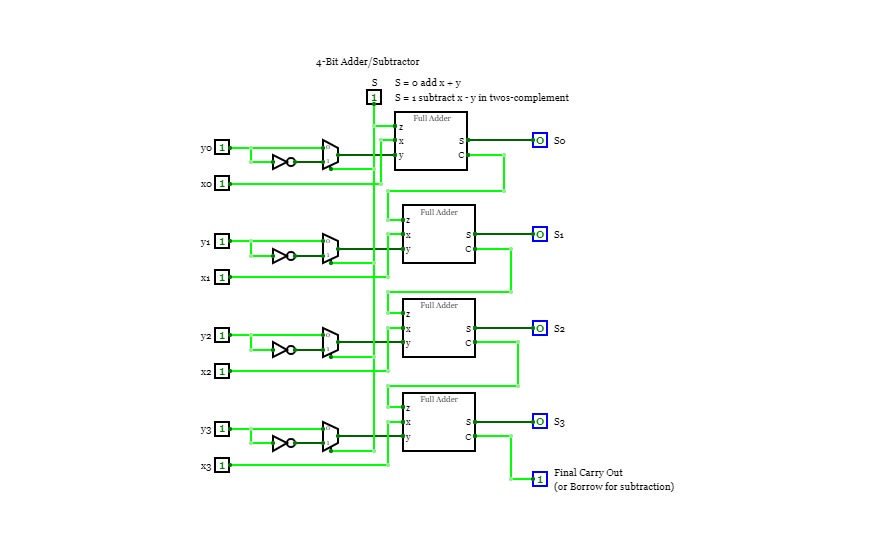
3.6 (Extra Credit)
3.6 (Extra Credit)Take the adder/subtractor circuit in slide page 37 (of Chapter 4 slides) and modify its output to include also comparison capabilities (=, <, >) for the two input numbers.
Hint: notice that if x=y then x-y = 0 (check if all bits of result are 0). If xy then x-y>0 (check if x≠y and sign bit is 0).