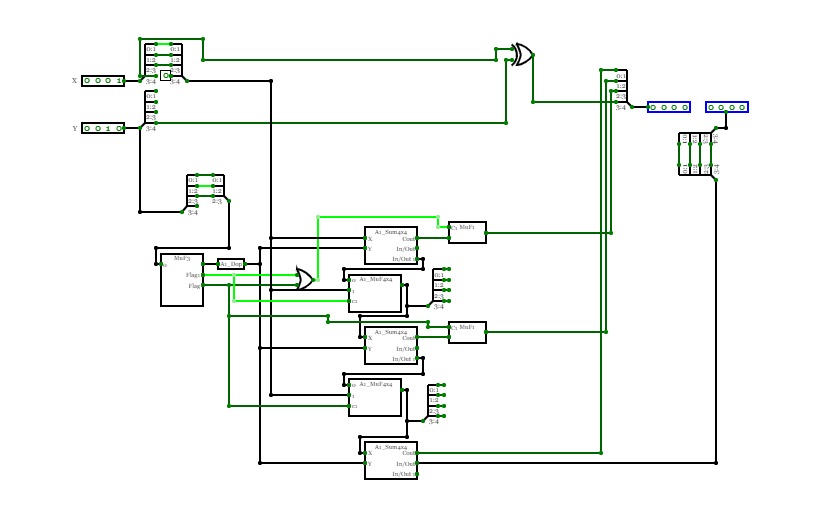
4-bit Devisor
4-bit DevisorDemonstration of a N x N divider with 4-bit numbers.
Description:
This project demonstrates a 4-bit divider capable of performing division on two 4-bit binary numbers. The circuit outputs both the quotient (Q) and the remainder (R) of the division. For instance, when dividing 14 by 3, the quotient will be 4 and the remainder (R) will be 2, as 14 = 3 * 4 + 2.
How It Works:
The divider operates by repeatedly subtracting the divisor from the dividend, shifting bits as necessary to align with binary division principles. The quotient is accumulated as the divisor is successfully subtracted from the dividend without the result going negative. The remainder (R) is what’s left of the dividend after the final subtraction, representing the "rest" of the division. This circuit is designed using a combination of adders and control logic to automate this process, illustrating fundamental digital division concepts.
BinaryDivision
BinaryDivisionImplementation of division via subtraction.