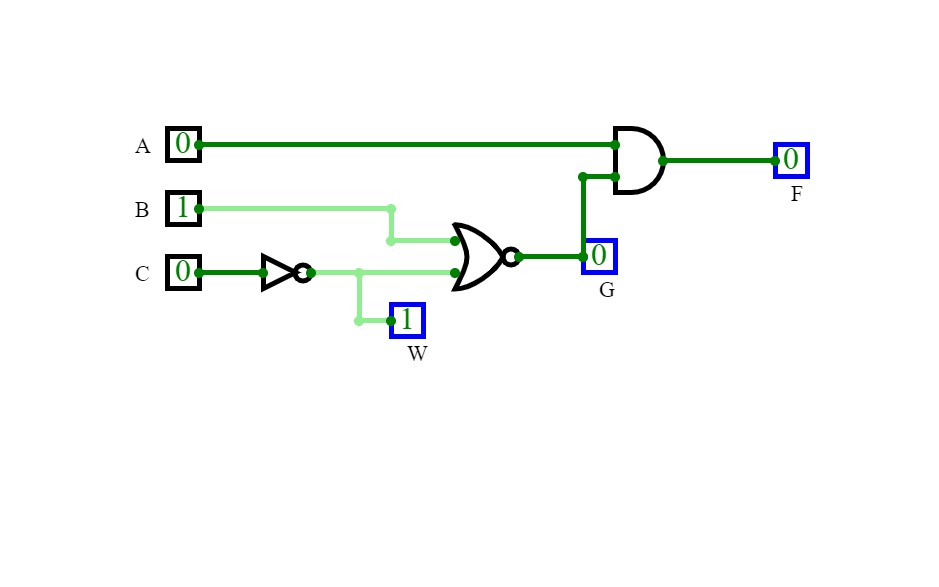
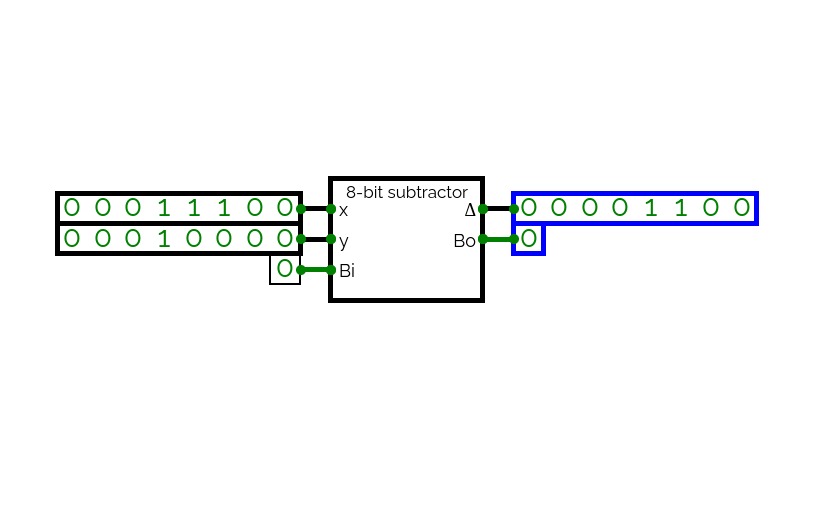
CombinationalLogic
CombinationalLogicsubtractor
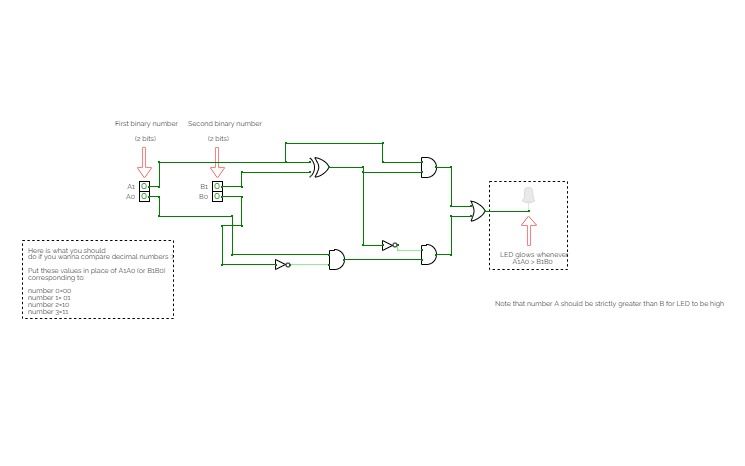
subtractorNumbers comparison circuit (2 - bit)
Numbers comparison circuit (2 - bit)ABOUT
This is a very simple number comparator circuit.
You input 2 numbers and it gives an output
whether A > B (both are 2-bit numbers)
(A should be strictly greater than B)
Note that A and B are both 2-bit binary numbers. Binary meaning that they are represented with only 1s and 0s.
Remark: Even if you don't know about binary numbers, I have got you covered :)
Simply refer to the table given in the circuit to work out the input yourself.
How to use?
Change the first input number labelled as A1 A0 by toggling the input. Similarly change the second number. Observe the LED for each combination of 2 numbers.
OUTPUT
You will see an LED glowing if A > B. Otherwise, you won't see any output.
eg. If you input A1A0 as 11 and B1B0 as 10, the LED would glow.
How I came up with the circuit?
Or rather you would ask, how can I design such a circuit myself? Well I will explain. So this is called a combinational circuit. You can design your circuit by first making a truth table with inputs as your two 2-bit numbers (4 inputs in total) and thinking about output for each set of inputs. So, you would have 42 =16 total inputs in your truth table.
Next, after you have mapped your input and then your output for all those inputs, you would be solving a logical expression for output Y for a given set of 4 inputs A1A0 B1B00.
You can use any method to solve for Y. You can use a K-map based reduction or you can simply solve using basic logic identities.
Once you get an expression (expression means something like this say (for eg. this is not what you may get) Y= A1.B1'+B1'B0'+...)
, you would then realize the circuit using logic gates. Just as I have done.
What you can try to do afterwards
Increase the input to 3-bits , 4-bits and so on...